
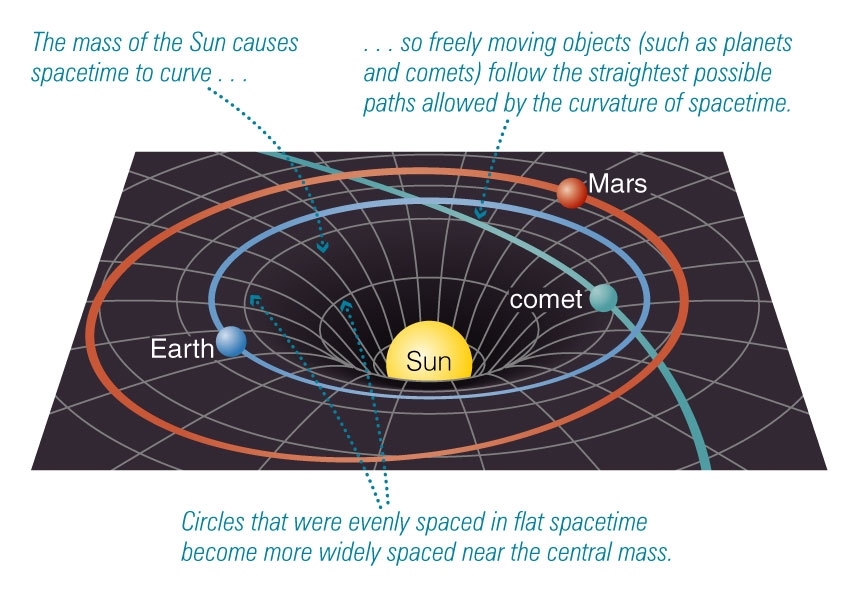
But crystals that assemble on closed surfaces are required by topology to have a minimum number of lattice defects, called disclinations, that act as conserved topological charges consider the 12 pentagons on a soccer ball or the 12 pentamers in a viral capsid.
The best-understood crystal ordering transition is that of two-dimensional freezing, which proceeds by the rapid eradication of lattice defects as the temperature is lowered below a critical threshold. Our results provide insights into the wetting and stability of shaped liquid filaments in simple and complex geometries relevant to applications ranging from printing to digital microfluidic devices. Mode selection between instability pathways to these different final states is achieved by dielectrophoresis forces selectively polarising the dipoles at the solid-liquid interface and so changing both the mobility of the contact line and the partial wetting of the topologically distinct liquid domains. Here, we show how controlling the static and dynamic wetting of a surface can lead to repeatable switching between a toroidal film of an electrically insulating liquid and patterns of droplets of well-defined dimensions confined to a ring geometry. When the filament is resting on a flat solid surface which imposes wetting conditions the subtle interplay with the fluid dynamics makes the instability pathways and mode selection difficult to predict. The breakup of a slender filament of liquid driven by surface tension is a classical fluid dynamics stability problem that is important in many situations where fine droplets are required.


 0 kommentar(er)
0 kommentar(er)
